Back to Article
Demonstration of metaweb embedding using RDPG
Download Notebook

Demonstration of metaweb embedding using RDPG

In [118]:
using EcologicalNetworks
using CairoMakie
using LinearAlgebra
import CSV
using DataFrames
using DataFramesMeta
CairoMakie.activate!(; px_per_unit = 2)

The first step is to load a series of bipartite quantitative networks between hosts and parasites, coming from the Hadfield et al. paper on host-parasite phylogenetic structure.

In [119]:
ids = getfield.(filter(n -> contains("Hadfield")(n.Reference), web_of_life()), :ID)
51-element Vector{SubString{String}}:
 "A_HP_001"
 "A_HP_002"
 "A_HP_003"
 "A_HP_004"
 "A_HP_005"
 "A_HP_006"
 "A_HP_007"
 "A_HP_008"
 "A_HP_009"
 "A_HP_010"
 ⋮
 "A_HP_043"
 "A_HP_044"
 "A_HP_045"
 "A_HP_046"
 "A_HP_047"
 "A_HP_048"
 "A_HP_049"
 "A_HP_050"
 "A_HP_051"

We convert these networks to binary bipartite networks, in order to make the metaweb aggregation easier.

In [120]:
N = [convert(BipartiteNetwork, web_of_life(n)) for n in ids]
51-element Vector{BipartiteNetwork{Bool, String}}:
 18×10 (String) bipartite ecological network (L: 61 - Bool)
 24×18 (String) bipartite ecological network (L: 96 - Bool)
 9×23 (String) bipartite ecological network (L: 108 - Bool)
 21×6 (String) bipartite ecological network (L: 52 - Bool)
 13×7 (String) bipartite ecological network (L: 51 - Bool)
 37×16 (String) bipartite ecological network (L: 123 - Bool)
 17×8 (String) bipartite ecological network (L: 43 - Bool)
 24×8 (String) bipartite ecological network (L: 37 - Bool)
 22×14 (String) bipartite ecological network (L: 97 - Bool)
 31×18 (String) bipartite ecological network (L: 88 - Bool)
 ⋮
 29×9 (String) bipartite ecological network (L: 73 - Bool)
 26×27 (String) bipartite ecological network (L: 197 - Bool)
 16×7 (String) bipartite ecological network (L: 57 - Bool)
 39×17 (String) bipartite ecological network (L: 202 - Bool)
 26×11 (String) bipartite ecological network (L: 100 - Bool)
 14×12 (String) bipartite ecological network (L: 71 - Bool)
 19×5 (String) bipartite ecological network (L: 39 - Bool)
 35×27 (String) bipartite ecological network (L: 226 - Bool)
 26×13 (String) bipartite ecological network (L: 107 - Bool)

Transforming the array of networks into a metaweb is done through the union operation:

In [121]:
M = reduce(∪, N)
206×121 (String) bipartite ecological network (L: 2131 - Bool)

In order to identify the pairs of species that have never been observed together, we use the following loop to create a co-occurence matrix:

In [122]:
C = zeros(Int64, size(M))
for n in N
    i = indexin(species(n; dims = 1), species(M; dims = 1))
    j = indexin(species(n; dims = 2), species(M; dims = 2))
    C[i, j] .+= 1
end

Before moving forward with the results, we will setup the multi-panel figure used in main text:

In [123]:
figure1 = Figure(; resolution = (950, 800))
figure1a = Axis(
    figure1[1, 1];
    xlabel = "Rank",
    ylabel = "L2 loss",
    title = "A",
    titlealign = :left,
)
figure1b = Axis(
    figure1[1, 2];
    xlabel = "Rank",
    ylabel = "Variance explained",
    title = "B",
    titlealign = :left,
)
figure1c = Axis(
    figure1[2, 1];
    xlabel = "Dimension 1",
    ylabel = "Dimension 2",
    title = "C",
    titlealign = :left,
)
figure1d = Axis(
    figure1[2, 2];
    xlabel = "Predicted weight",
    ylabel = "Density",
    title = "D",
    titlealign = :left,
)
current_figure()

The first thing we want to do is measure the L2 loss (the sum of squared errors) as a function of the rank. The rank of the metaweb is at most the number of species on its least species-rich side:

In [124]:
rank(adjacency(M))
121

The following list comprehension will perform the RDPG embedding for each rank between 1 and the rank of the metaweb, then multiply the left/right subspaces together to get an approximated network, and report the per-interaction averaged L2 error:

In [125]:
rnk = collect(1:rank(adjacency(M)))
L2 = [sum((adjacency(M) - prod(rdpg(M, r))) .^ 2) ./ prod(size(M)) for r in rnk]
121-element Vector{Float64}:
 0.05744130057895759
 0.0488201549717561
 0.044182471764921294
 0.04014623856002384
 0.03731319071666472
 0.035036091173708594
 0.033129096411421304
 0.03128810293334584
 0.029824448518954886
 0.028485820019597416
 ⋮
 4.756534964035326e-5
 3.871435018435366e-5
 3.077568517320694e-5
 2.3762477728538295e-5
 1.728209478741771e-5
 1.1040542326391507e-5
 5.9908504730463834e-6
 2.6163841056681962e-6
 3.383682609541635e-30

We add this to the first panel of the figure:

In [126]:
lines!(figure1a, rnk, L2; color = :black)
current_figure()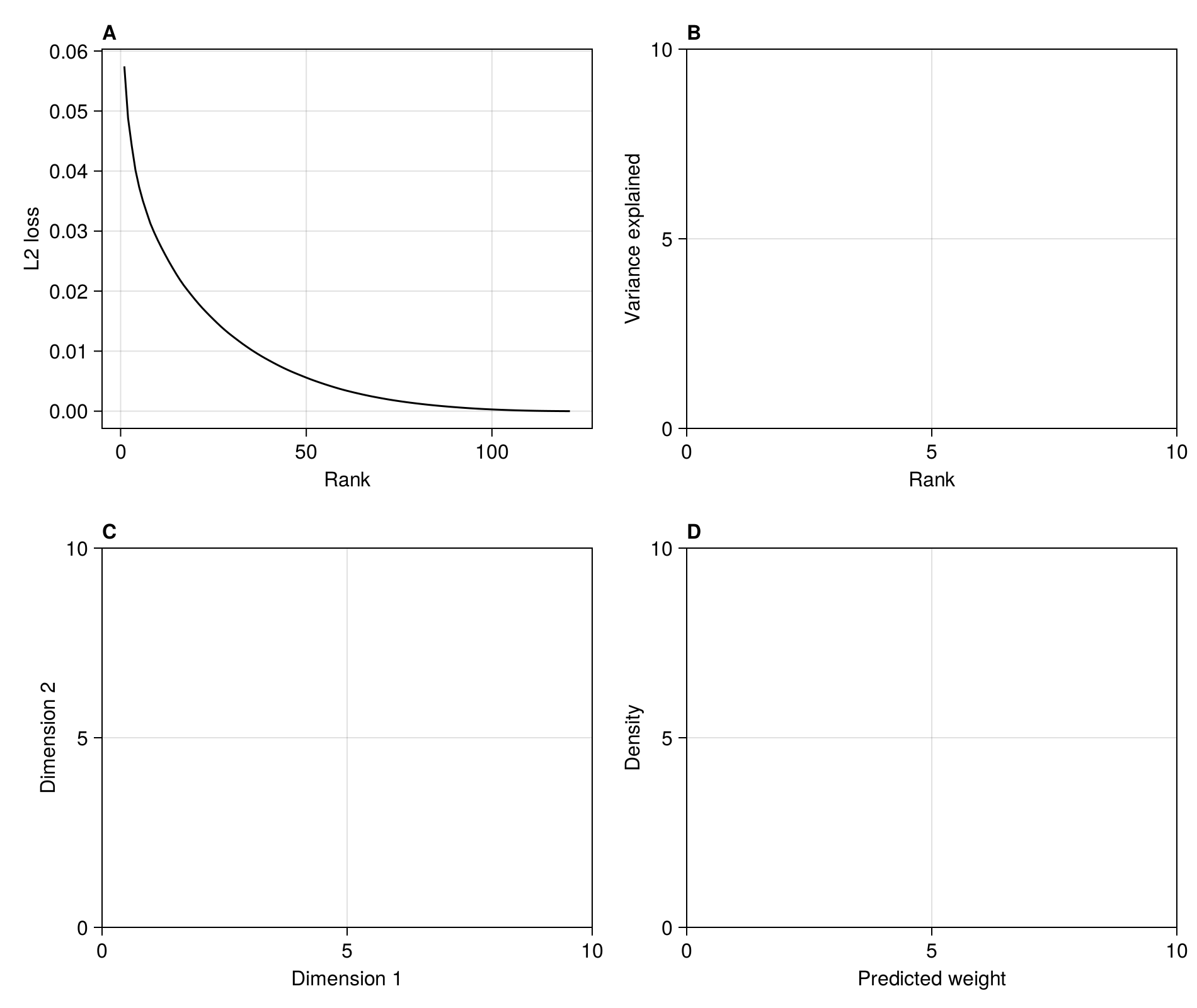

In order to identify the point of inflexion at which to perform the embedding, we could calculate the second order derivate of the loss function w.r.t. rank, using the approximation provided by the finite differences method, for which there are closed form solutions for the first (forward difference), last (backward difference), and any (central difference point). This can be done on the singular values of the SVD yielding the RDPG used for the embedding:

In [127]:
singularvalues = svd(adjacency(M)).S
lines!(
    figure1b,
    rnk,
    cumsum(singularvalues) ./ sum(singularvalues); color = :black,
)
current_figure()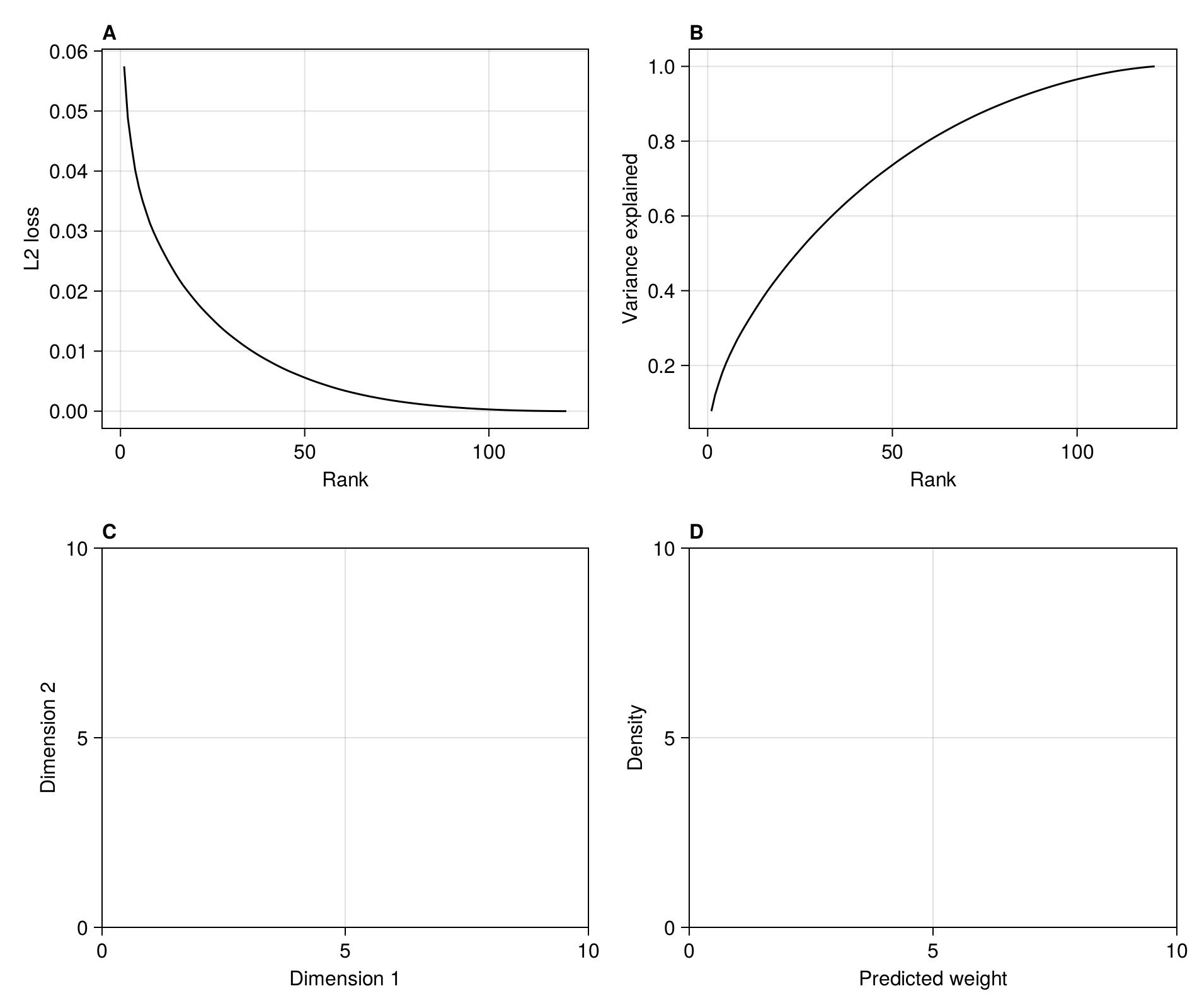

The finite differences methods to get the inflexion points proper is simply given by:

In [128]:
sv = copy(singularvalues)
D = zeros(size(L2))
for i in axes(D, 1)
    if i == 1
        D[i] = sv[i + 2] - 2sv[i + 1] + sv[i]
    elseif i == length(D)
        D[i] = sv[i] - 2sv[i - 1] + sv[i - 2]
    else
        D[i] = sv[i + 1] - 2sv[i] + sv[i - 1]
    end
end

In practice, the screeplot of variance explained by each rank is noisy, meaning that the correct inflexion point is not necessarilly obvious from the series of second order derivatives (themselves an approximation due to the finite differences method). Here, we are placing the inflexion point at the value that is closest to 0 (in absolute value) - this is a slightly conservative approach that will keep more dimensions, but provide a better approximation of the network.

In [129]:
embedding_rank = last(findmin(abs.(D)))
39

We can add it to the figure:

In [130]:
scatter!(figure1a, [embedding_rank], [L2[embedding_rank]]; color = :black)
scatter!(
    figure1b,
    [embedding_rank],
    [(cumsum(singularvalues) ./ sum(singularvalues))[embedding_rank]];
    color = :black,
)
Scatter{Tuple{Vector{Point{2, Float32}}}}

In the next steps, we will perform the RDPG embedding at this rank. We can check the L2 loss associated with this representation:

In [131]:
L2[embedding_rank]
0.008781432658004353

The left/right subspaces are given by the rdpg function, which internally performs a t-SVD and then multiply each side by the square root of the eigenvalues:

In [132]:
L, R = rdpg(M, embedding_rank)
([-0.31286375720303533 -0.043030881301210994 … 0.13089538016786548 -0.20429603515164355; -0.13639064534793804 -0.069120397590513 … -0.022693347528150234 0.11122052820015549; … ; -0.07325950183520884 0.055523273646558215 … 0.009841316351827679 -0.01931207868006777; -0.037791712381080346 0.03795436890539979 … 0.07396177101652388 -0.10508157577475588], [-1.484396333351671 -0.6088099455780831 … -0.18331412712563155 -0.018557865543628753; -0.06204291742899854 0.07811536918416419 … -0.0649963044402432 -0.004540292268812767; … ; -0.15780083148368063 0.030858539181893643 … 0.23635721814746793 -0.039464787454680156; 0.11993993308033085 -0.2685421627054579 … 0.007877516594161235 0.10605965189104812])

Checking the sizes of the L and R subspaces is important. For example, the size of L is:

In [133]:
size(L)
(206, 39)

The number of rows (parasite richness) and columns (subspaces dimensions) is correct, so we can move on to the next step (doing the same exercise for R will show why the L*R multiplication will give back a matrix of the correct dimension). We will approximate the network at the previously identified rank, and call it P:

In [134]:
P = clamp.(L * R, 0., 1.)
206×121 Matrix{Float64}:
 1.0        1.0         0.199705    …  0.0854123   0.0360167   0.0
 1.0        1.0         0.49918        0.0130665   0.0         0.0
 0.869676   0.843036    0.347334       0.0         0.0275938   0.0
 0.995816   1.0         0.85884        0.0         0.0         0.0242046
 0.968721   1.0         0.198935       0.0342837   0.0         0.0
 1.0        1.0         0.805771    …  0.0894987   0.0         0.0670649
 0.116086   0.957751    0.149858       0.0375512   0.0         0.0
 0.950946   1.0         0.12715        0.0514532   0.0         0.0
 1.0        1.0         0.0514726      0.0         0.0454504   0.0850339
 1.0        0.938797    0.249431       0.0         0.0         0.0107727
 ⋮                                  ⋱                          ⋮
 0.0        0.0353385   0.0            0.0         0.00455419  0.0
 0.0        0.0353385   0.0            0.0         0.00455419  0.0
 0.0        0.0353385   0.0            0.0         0.00455419  0.0
 0.0        0.0353385   0.0         …  0.0         0.00455419  0.0
 1.0        0.0319898   0.040841       0.804289    0.907391    0.00389104
 0.0338076  0.0303734   0.00853267     0.0         0.0768271   0.0
 0.896346   0.00938109  0.0740001      0.0         0.0         0.0146878
 0.0112658  0.0359472   0.0            0.0         0.0         0.0
 0.03336    0.007738    0.0         …  0.00215311  0.0         0.0

With this matrix, we can start looking at the weight given for (i) positive interactions, (ii) interactions that are never observed but for which the species pair is observed at least once, and (iii) species pairs that are never observed. We simply plot the desntiy for each of these three situations and add it to the figure:

In [135]:
noc = density!(figure1d, P[findall(iszero.(C))])
pos = density!(figure1d, P[findall(adjacency(M))])
neg = density!(figure1d, P[findall(iszero.(adjacency(M)) .& .~iszero.(C))])
axislegend(
    figure1d,
    [pos, neg, noc],
    ["Interactions", "Non-interactions", "No co-occurence"],
)
Legend()

From this panel, it is rather clear that a lot of interactions without documented co-occurrence have a lower assigned weight, and are therefore less likely to be feasible. Turning this information into a prediction of interaction existence can be carried out as a binary classification exercise using e.g. weight thresholding.

Another potentially useful visualisation is to look at the position of each species on the first/second dimension of the relevant subspace.

In [136]:
para = scatter!(figure1c, L[:, 1], L[:, 2]; marker = :rect)
host = scatter!(figure1c, R'[:, 1], R'[:, 2])
axislegend(figure1c, [para, host], ["Parasites", "Hosts"]; position = :lb)
current_figure()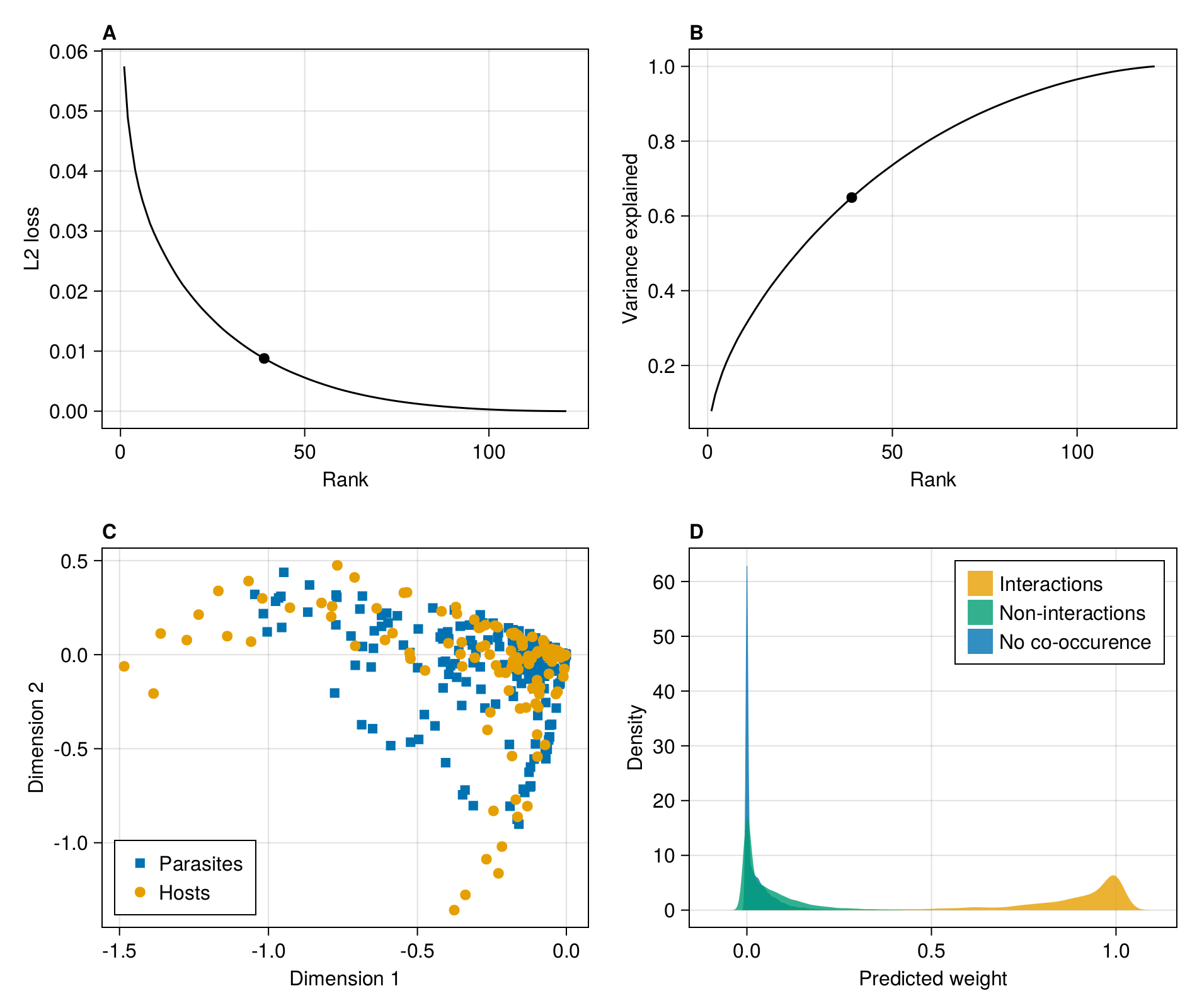

We finally save a high-dpi version of the first figure to disk:

In [137]:
current_figure()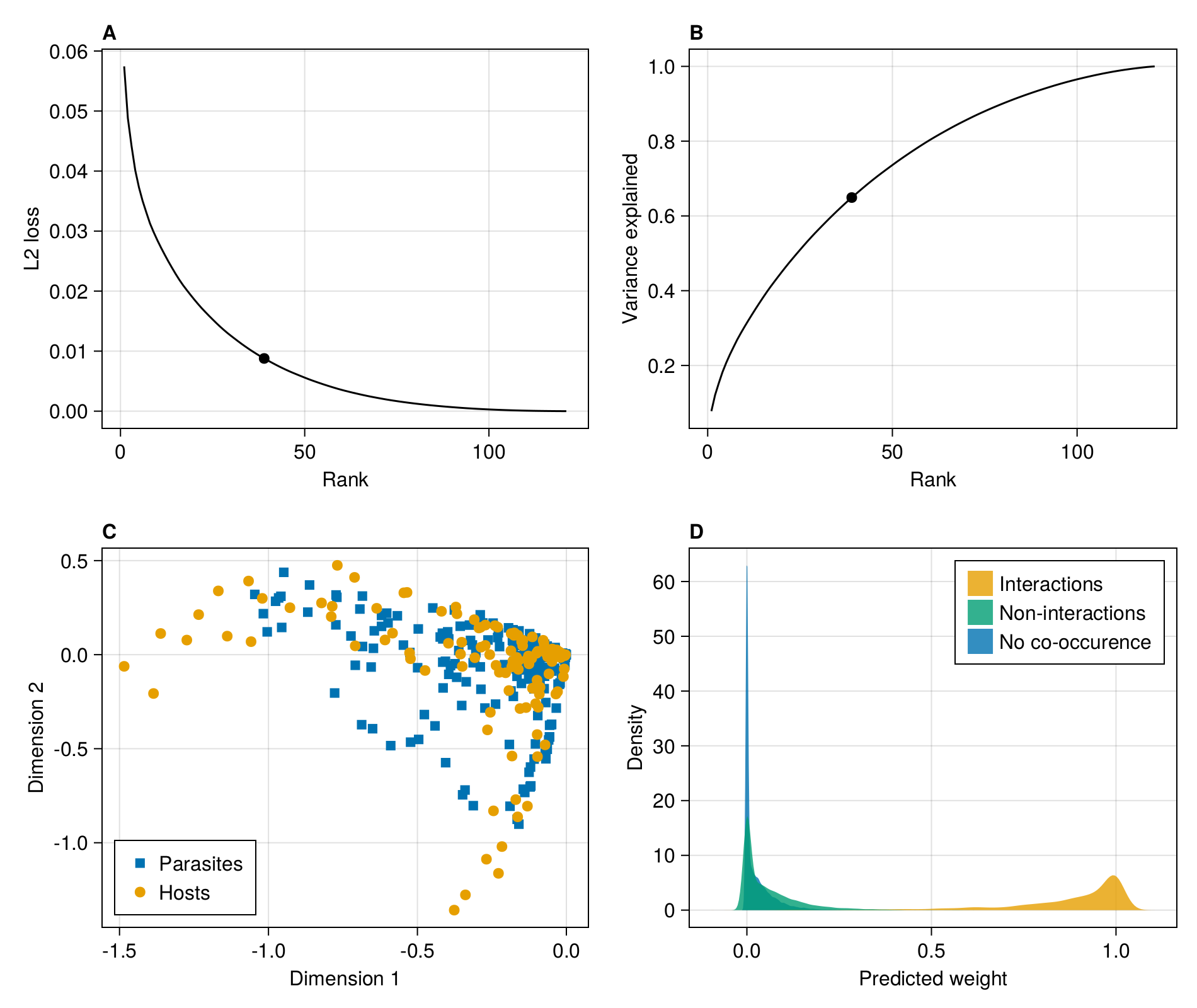

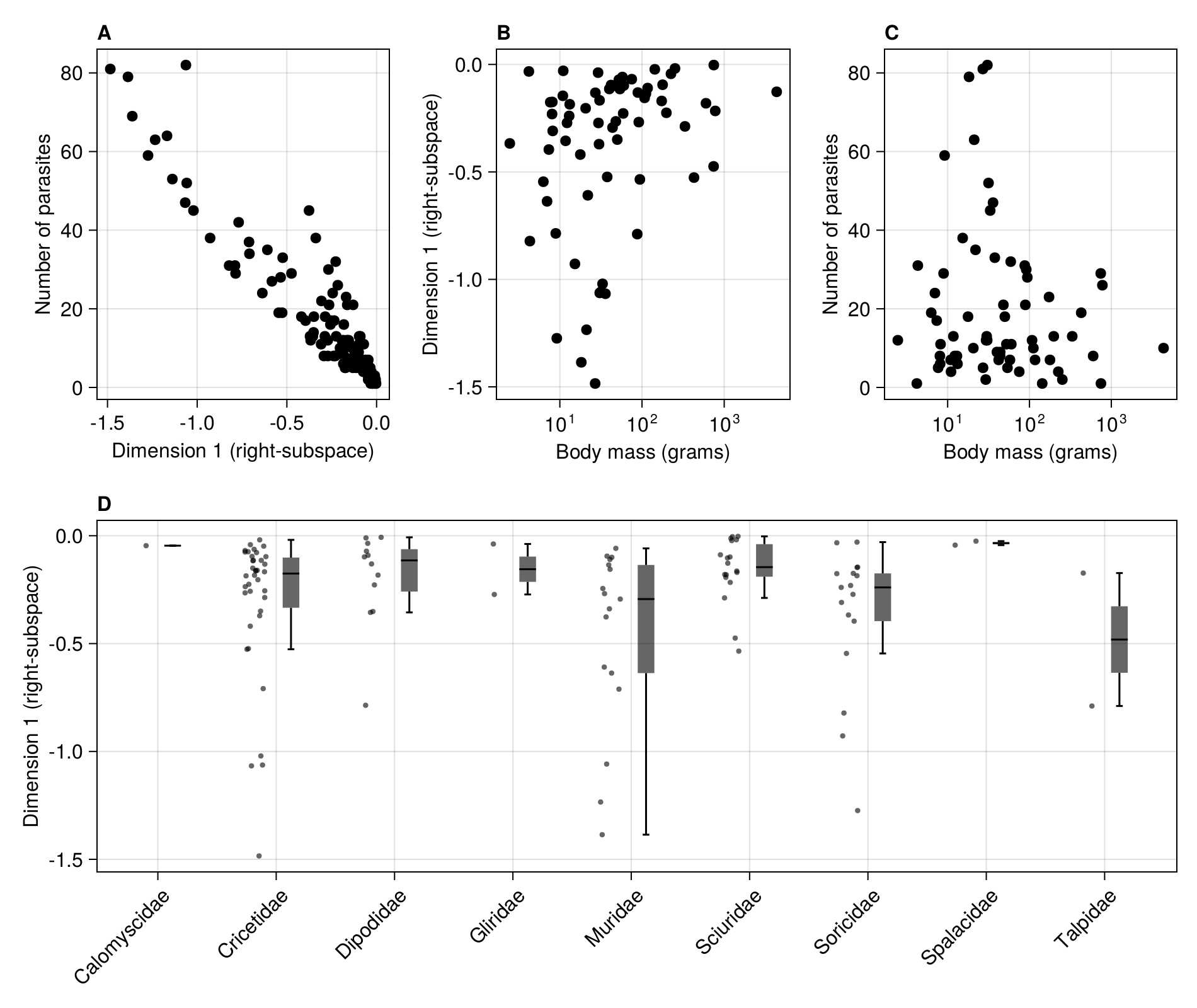
Figure 1: Validation of an embedding for a host-parasite metaweb, using Random Dot Product Graphs. A, decrease in approximation error as the number of dimensions in the subspaces increases. B, increase in cumulative variance explained as the number of ranks considered increases; in A and B, the dot represents the point of inflexion in the curve (at rank 39) estimated using the finite differences method. C, position of hosts and parasites in the space of latent variables on the first and second dimensions of their respective subspaces (the results have been clamped to the unit interval). D, predicted interaction weight from the RDPG based on the status of the species pair in the metaweb.

In the second figure, we will relate the embedding information to taxonomic/ecological information about the species, using hosts as an illustration:

In [138]:
figure2 = Figure(; resolution = (950, 800))
figure2a = Axis(
    figure2[1, 1];
    xlabel = "Dimension 1 (right-subspace)",
    ylabel = "Number of parasites",
    title = "A",
    titlealign = :left,
)
figure2b = Axis(
    figure2[1, 2];
    ylabel = "Dimension 1 (right-subspace)",
    xlabel = "Body mass (grams)",
    xscale = log10,
    title = "B",
    titlealign = :left,
)
figure2c = Axis(
    figure2[1, 3];
    ylabel = "Number of parasites",
    xlabel = "Body mass (grams)",
    xscale = log10,
    title = "C",
    titlealign = :left,
)
figure2d = Axis(
    figure2[2, 1:3];
    ylabel = "Dimension 1 (right-subspace)",
    title = "D",
    titlealign = :left,
    xticklabelrotation = π / 4,
)
current_figure()

We can now link the position on the first dimension to ecologically relevant information, like e.g. the number of parasites.

In [139]:
scatter!(figure2a, R[1, :], vec(sum(adjacency(M); dims = 1)); color = :black)
current_figure()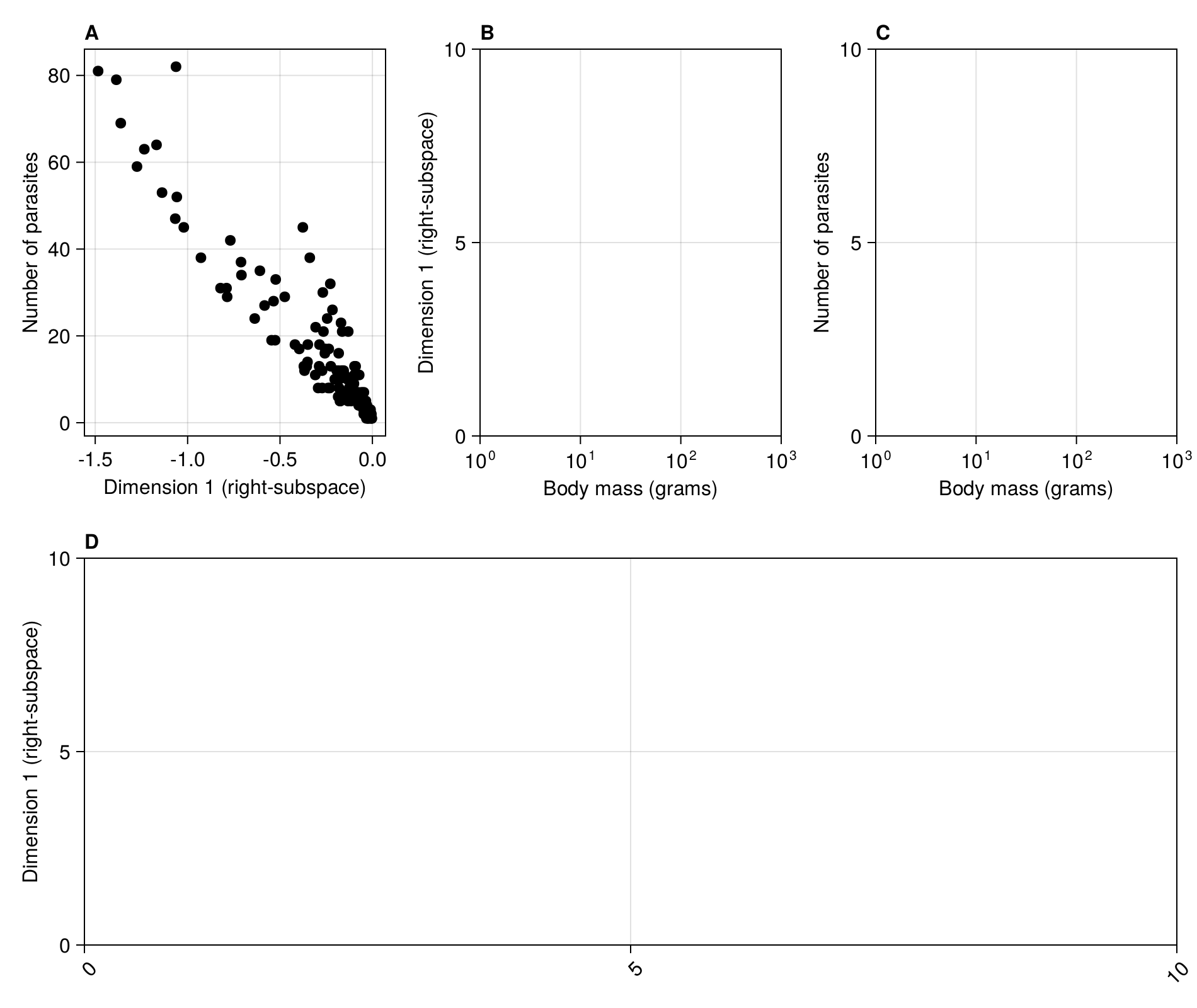

We will now load the PanTHERIA database to get metadata and functional traits on host species:

In [140]:
pantheria = DataFrame(CSV.File(joinpath("..", "code", "PanTHERIA_1-0_WR05_Aug2008.txt")))
5416×55 DataFrame
5391 rows omitted
Row MSW05_Order MSW05_Family MSW05_Genus MSW05_Species MSW05_Binomial 1-1_ActivityCycle 5-1_AdultBodyMass_g 8-1_AdultForearmLen_mm 13-1_AdultHeadBodyLen_mm 2-1_AgeatEyeOpening_d 3-1_AgeatFirstBirth_d 18-1_BasalMetRate_mLO2hr 5-2_BasalMetRateMass_g 6-1_DietBreadth 7-1_DispersalAge_d 9-1_GestationLen_d 12-1_HabitatBreadth 22-1_HomeRange_km2 22-2_HomeRange_Indiv_km2 14-1_InterbirthInterval_d 15-1_LitterSize 16-1_LittersPerYear 17-1_MaxLongevity_m 5-3_NeonateBodyMass_g 13-2_NeonateHeadBodyLen_mm 21-1_PopulationDensity_n/km2 10-1_PopulationGrpSize 23-1_SexualMaturityAge_d 10-2_SocialGrpSize 24-1_TeatNumber 12-2_Terrestriality 6-2_TrophicLevel 25-1_WeaningAge_d 5-4_WeaningBodyMass_g 13-3_WeaningHeadBodyLen_mm References 5-5_AdultBodyMass_g_EXT 16-2_LittersPerYear_EXT 5-6_NeonateBodyMass_g_EXT 5-7_WeaningBodyMass_g_EXT 26-1_GR_Area_km2 26-2_GR_MaxLat_dd 26-3_GR_MinLat_dd 26-4_GR_MidRangeLat_dd 26-5_GR_MaxLong_dd 26-6_GR_MinLong_dd 26-7_GR_MidRangeLong_dd 27-1_HuPopDen_Min_n/km2 27-2_HuPopDen_Mean_n/km2 27-3_HuPopDen_5p_n/km2 27-4_HuPopDen_Change 28-1_Precip_Mean_mm 28-2_Temp_Mean_01degC 30-1_AET_Mean_mm 30-2_PET_Mean_mm
String31 String31 String31 String31 String Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Int64 Float64 Int64 Float64 Float64 Float64 String Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Float64 Int64 Float64 Float64 Float64 Float64 Float64 Float64 Float64
1 Artiodactyla Camelidae Camelus dromedarius Camelus dromedarius 3.0 4.92714e5 -999.0 -999.0 -999.0 1651.62 40293.0 407000.0 3.0 -999.0 386.51 1.0 196.32 -999.0 614.41 0.98 1.0 480.0 36751.2 -999.0 0.98 11.0 1947.94 10.0 -999 1.0 1 389.38 -999.0 -999.0 511;543;719;1274;1297;1594;1654;1822;1848;2655;3044 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0
2 Carnivora Canidae Canis adustus Canis adustus 1.0 10392.5 -999.0 745.32 -999.0 -999.0 -999.0 -999.0 6.0 329.99 65.0 1.0 1.01 1.01 -999.0 4.5 -999.0 137.0 -999.0 -999.0 0.74 -999.0 249.88 -999.0 8 1.0 2 52.89 -999.0 -999.0 542;543;730;1113;1297;1573;2655 -999.0 -999.0 -999.0 -999.0 1.05814e7 16.72 -28.73 -6.0 43.55 -17.53 13.0 0 35.2 1.0 0.14 90.75 236.51 922.9 1534.4
3 Carnivora Canidae Canis aureus Canis aureus 2.0 9658.7 -999.0 827.53 7.5 -999.0 -999.0 -999.0 6.0 -999.0 61.24 1.0 2.95 3.13 365.0 3.74 -999.0 192.0 211.82 -999.0 0.22 -999.0 371.23 -999.0 8 1.0 2 61.3 -999.0 -999.0 543;679;730;1113;1297;1573;2655 -999.0 1.1 -999.0 -999.0 2.57395e7 47.0 -4.71 21.14 108.54 -17.05 45.74 0 79.29 0.0 0.1 44.61 217.23 438.02 1358.98
4 Carnivora Canidae Canis latrans Canis latrans 2.0 11989.1 -999.0 872.39 11.94 365.0 3699.0 10450.0 1.0 255.0 61.74 1.0 18.88 19.91 365.0 5.72 -999.0 262.0 200.01 -999.0 0.25 -999.0 372.9 -999.0 8 1.0 3 43.71 -999.0 -999.0 367;542;543;730;1113;1297;1573;1822;2655 -999.0 1.1 -999.0 -999.0 1.70991e7 71.39 8.02 39.7 -67.07 -168.12 -117.6 0 27.27 0.0 0.06 53.03 58.18 503.02 728.37
5 Carnivora Canidae Canis lupus Canis lupus 2.0 31756.5 -999.0 1055.0 14.01 547.5 11254.2 33100.0 1.0 180.0 63.5 1.0 159.86 43.13 365.0 4.98 2.0 354.0 412.31 -999.0 0.01 -999.0 679.37 -999.0 9 1.0 3 44.82 -999.0 -999.0 367;542;543;730;1015;1052;1113;1297;1573;1594;2338;2655 -999.0 -999.0 -999.0 -999.0 5.08034e7 83.27 11.48 47.38 179.65 -171.84 3.9 0 37.87 0.0 0.04 34.79 4.82 313.33 561.11
6 Artiodactyla Bovidae Bos frontalis Bos frontalis 2.0 8.00143e5 -999.0 2700.0 -999.0 -999.0 -999.0 -999.0 3.0 -999.0 273.75 -999.0 -999.0 -999.0 403.02 1.22 1.0 314.4 22977.0 -999.0 0.54 -999.0 610.97 40.0 -999 -999.0 1 186.67 -999.0 -999.0 511;543;730;899;1297;1525;1848;2655;2986 -999.0 -999.0 -999.0 -999.0 2.29433e6 28.01 2.86 15.43 108.68 73.55 91.12 1 152.67 8.0 0.09 145.21 229.71 1053.45 1483.02
7 Artiodactyla Bovidae Bos grunniens Bos grunniens -999.0 500000.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 2.0 -999.0 273.75 -999.0 -999.0 -999.0 -999.0 1.0 1.0 267.0 -999.0 -999.0 -999.0 -999.0 755.15 110.0 -999 -999.0 1 243.33 -999.0 -999.0 511;899;1297;1525;1848;2655 -999.0 -999.0 -999.0 -999.0 1.52354e6 38.88 29.66 34.27 99.23 75.91 87.57 0 2.03 0.0 0.05 30.41 -59.31 246.2 732.74
8 Artiodactyla Bovidae Bos javanicus Bos javanicus 2.0 6.35974e5 -999.0 2075.0 -999.0 912.5 -999.0 -999.0 2.0 -999.0 296.78 1.0 -999.0 -999.0 -999.0 1.22 1.0 318.96 -999.0 -999.0 0.75 21.0 797.31 40.0 -999 1.0 1 287.74 -999.0 -999.0 511;730;899;1297;1525;1848;2152;2655 -999.0 -999.0 -999.0 -999.0 1.68792e6 25.08 -8.78 8.15 118.35 94.94 106.64 1 139.21 4.0 0.11 187.69 239.18 1301.28 1592.26
9 Primates Pitheciidae Callicebus cupreus Callicebus cupreus 3.0 1117.02 -999.0 354.99 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 129.25 1.0 -999.0 -999.0 395.41 1.01 -999.0 -999.0 73.6 -999.0 4.89 -999.0 -999.0 2.05 -999 2.0 -999 201.85 -999.0 -999.0 1544;1547;1605;1633;1848;2151;2251;2344;2655;2986 -999.0 1.05 -999.0 -999.0 6.90923e5 -2.5 -10.67 -6.58 -61.59 -74.92 -68.25 0 1.07 0.0 0.05 196.01 255.36 1529.55 1573.18
10 Primates Pitheciidae Callicebus discolor Callicebus discolor -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 -999.0 -999 -999.0 -999.0 -999.0 -999 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0
11 Primates Pitheciidae Callicebus donacophilus Callicebus donacophilus 3.0 897.67 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 1.0 -999.0 -999.0 -999.0 1.02 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 1.0 -999 2.0 -999 -999.0 -999.0 -999.0 1547;1605;1633;2151;2655 -999.0 -999.0 -999.0 -999.0 288759.0 -10.45 -21.29 -15.87 -57.52 -67.21 -62.37 0 3.63 0.0 0.17 108.93 244.32 1238.19 1469.11
12 Primates Pitheciidae Callicebus dubius Callicebus dubius 3.0 992.4 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 1.0 -999.0 -999.0 -999.0 1.02 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 1.0 -999 2.0 -999 -999.0 -999.0 -999.0 1605;1633;2151;2655 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0
13 Primates Pitheciidae Callicebus hoffmannsi Callicebus hoffmannsi 3.0 1067.61 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 1.0 -999.0 -999.0 -999.0 1.02 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 1.0 -999 2.0 -999 -999.0 -999.0 -999.0 1547;1605;1633;2151;2655 -999.0 -999.0 -999.0 -999.0 98076.5 -1.95 -6.0 -3.97 -54.87 -59.21 -57.04 0 2.6 0.0 0.1 158.41 258.18 1417.63 1610.4
⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮
5405 Rodentia Muridae Zelotomys hildegardeae Zelotomys hildegardeae -999.0 55.22 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 5.75 -999.0 -999.0 -999.0 -999.0 61.11 -999.0 -999.0 -999.0 -999 -999.0 -999 -999.0 -999.0 -999.0 730;1297;2655 -999.0 -999.0 -999.0 -999.0 3.21796e6 5.8 -14.1 -4.15 40.18 14.4 27.29 0 40.05 2.0 0.17 101.6 220.68 1045.09 1519.34
5406 Rodentia Muridae Zelotomys woosnami Zelotomys woosnami -999.0 54.1 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 30.99 -999.0 -999.0 -999.0 31.0 4.99 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 -999.0 -999 15.9 -999.0 -999.0 1297;2655 -999.0 3.83 -999.0 -999.0 5.57093e5 -17.49 -27.63 -22.56 26.62 14.83 20.73 0 2.08 0.0 0.1 32.83 214.54 461.02 1464.56
5407 Rodentia Anomaluridae Zenkerella insignis Zenkerella insignis -999.0 200.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 2.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 2.0 -999 -999.0 -999.0 -999.0 511;2655 -999.0 -999.0 -999.0 -999.0 1.71071e5 4.57 1.65 3.11 16.89 9.62 13.26 1 20.37 1.0 0.05 151.21 238.98 1342.66 1488.96
5408 Cetacea Ziphiidae Ziphius cavirostris Ziphius cavirostris -999.0 4.775e6 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 1.0 -999.0 -999.0 1.0 -999.0 -999.0 -999.0 1.0 -999.0 432.0 -999.0 -999.0 -999.0 2.0 -999.0 -999.0 -999 -999.0 3 -999.0 -999.0 -999.0 172;543;1297;2151;2655 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0
5409 Rodentia Cricetidae Zygodontomys brevicauda Zygodontomys brevicauda 1.0 52.22 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 3.0 -999.0 25.39 1.0 -999.0 -999.0 25.0 4.23 5.5 -999.0 3.54 -999.0 1029.29 -999.0 42.69 -999.0 -999 1.0 2 18.5 21.99 -999.0 730;1297;2151;2159;2655 -999.0 -999.0 -999.0 -999.0 2.46036e6 11.58 0.16 5.87 -51.65 -83.74 -67.7 0 32.13 0.0 0.12 163.89 243.08 1462.12 1666.76
5410 Rodentia Cricetidae Zygodontomys brunneus Zygodontomys brunneus -999.0 75.59 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 -999.0 -999 -999.0 -999.0 -999.0 2655 -999.0 -999.0 -999.0 -999.0 91161.4 7.46 1.15 4.31 -73.5 -77.64 -75.57 7 116.18 13.0 0.09 150.38 195.09 1502.65 1553.88
5411 Rodentia Geomyidae Zygogeomys trichopus Zygogeomys trichopus -999.0 473.54 -999.0 225.0 -999.0 -999.0 -999.0 -999.0 4.0 -999.0 -999.0 2.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 1.0 1 -999.0 -999.0 -999.0 1015;2151;2655 -999.0 -999.0 -999.0 -999.0 1706.58 19.74 19.26 19.5 -101.67 -102.41 -102.04 83 105.64 83.0 0.05 84.67 176.37 833.34 1362.0
5412 Rodentia Muridae Zyzomys argurus Zyzomys argurus -999.0 40.42 -999.0 107.83 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 25.0 -999.0 0.00103959 0.000956472 219.0 2.76 -999.0 -999.0 -999.0 -999.0 535.51 -999.0 155.06 -999.0 4 -999.0 -999 34.99 14.0 81.25 435;456;525;730;1297;2655;2803 -999.0 1.42 -999.0 -999.0 8.86981e5 -11.11 -25.49 -18.3 147.85 114.33 131.09 0 1.1 0.0 0.02 62.33 256.75 692.93 1704.98
5413 Rodentia Muridae Zyzomys maini Zyzomys maini -999.0 93.99 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 -999.0 -999 -999.0 -999.0 -999.0 2655 -999.0 -999.0 -999.0 -999.0 51093.3 -12.9 -15.06 -13.98 133.87 131.45 132.66 0 0.17 0.0 0.0 90.76 265.3 877.9 1755.73
5414 Rodentia Muridae Zyzomys palatilis Zyzomys palatilis -999.0 123.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 -999.0 -999 -999.0 -999.0 -999.0 2655 -999.0 -999.0 -999.0 -999.0 4667.41 -17.45 -18.16 -17.81 137.43 136.72 137.08 0 0.0 0.0 -999.0 49.0 247.16 637.9 1638.67
5415 Rodentia Muridae Zyzomys pedunculatus Zyzomys pedunculatus -999.0 100.0 -999.0 126.79 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 4 -999.0 -999 -999.0 -999.0 -999.0 2655;2803 -999.0 -999.0 -999.0 -999.0 233916.0 -20.25 -25.36 -22.81 135.78 130.16 132.97 0 0.09 0.0 0.25 21.64 215.72 291.82 1405.85
5416 Rodentia Muridae Zyzomys woodwardi Zyzomys woodwardi -999.0 95.02 -999.0 146.07 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 231.16 2.23 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 155.06 -999.0 4 -999.0 -999 34.99 -999.0 -999.0 525;1297;2655;2803 -999.0 1.38 -999.0 -999.0 70724.8 -13.73 -17.35 -15.54 127.69 123.42 125.55 0 0.0 0.0 -999.0 79.45 280.41 798.86 1765.19

We can match the PanTHERIA rows with species names, and extract the columns we will use: species name, family, position on the first dimension, and finally bodymass:

In [141]:
vidx = filter(!isnothing, indexin(species(M; dims = 2), pantheria.MSW05_Binomial))
rodents = pantheria[vidx, :]
species_index = indexin(rodents.MSW05_Binomial, species(M; dims = 2))
rodents.dim1 = R[1, species_index]
rodents.prich = [degree(M)[k] for k in rodents.MSW05_Binomial]

@select!(
    rodents,
    :species = :MSW05_Binomial,
    :family = :MSW05_Family,
    :dimension = :dim1,
    :parasites = :prich,
    :bodymass = $(Symbol("5-1_AdultBodyMass_g"))
)

rodents = @orderby(rodents, :family)
109×5 DataFrame
84 rows omitted
Row species family dimension parasites bodymass
String String31 Float64 Int64 Float64
1 Calomyscus mystax Calomyscidae -0.0460271 7 -999.0
2 Microtus arvalis Cricetidae -1.4844 81 26.9
3 Prometheomys schaposchnikowi Cricetidae -0.0686128 4 75.0
4 Microtus majori Cricetidae -0.186042 11 -999.0
5 Cricetulus migratorius Cricetidae -1.0629 82 30.59
6 Chionomys nivalis Cricetidae -0.0958455 7 42.01
7 Lagurus lagurus Cricetidae -0.2039 10 20.6
8 Cricetus cricetus Cricetidae -0.526361 19 428.95
9 Microtus oeconomus Cricetidae -1.02079 45 33.1
10 Microtus gregalis Cricetidae -0.708764 34 -999.0
11 Allocricetulus eversmanni Cricetidae -0.25523 17 -999.0
12 Ellobius talpinus Cricetidae -0.113965 9 40.0
13 Microtus agrestis Cricetidae -1.06681 47 35.87
⋮ ⋮ ⋮ ⋮ ⋮ ⋮
98 Sorex tundrensis Soricidae -0.17576 5 7.65
99 Diplomesodon pulchellum Soricidae -0.0295968 4 11.0
100 Sorex cinereus Soricidae -0.0326016 1 4.2
101 Sorex roboratus Soricidae -0.239524 8 12.99
102 Sorex alpinus Soricidae -0.230646 8 8.04
103 Neomys anomalus Soricidae -0.185322 6 13.19
104 Crocidura leucodon Soricidae -0.145881 7 10.88
105 Sorex asper Soricidae -0.146753 7 -999.0
106 Myospalax aspalax Spalacidae -0.025057 2 -999.0
107 Myospalax myospalax Spalacidae -0.0434989 4 225.0
108 Talpa europaea Talpidae -0.789351 31 87.53
109 Talpa altaica Talpidae -0.173096 5 -999.0

We can plot the positions on the first dimension by taxonomic family (outliers do not appear on the boxplots):

In [142]:
rainclouds!(
    figure2d,
    rodents.family,
    rodents.dimension;
    plot_boxplots = true,
    boxplot_width = 0.22,
    boxplot_nudge = 0.25,
    strokewidth = 0.0,
    clouds = nothing,
    datalimits = extrema,
    orientation = :vertical,
    markersize = 6,
    side_nudge = -0.125,
    jitter_width = 0.22,
)
current_figure()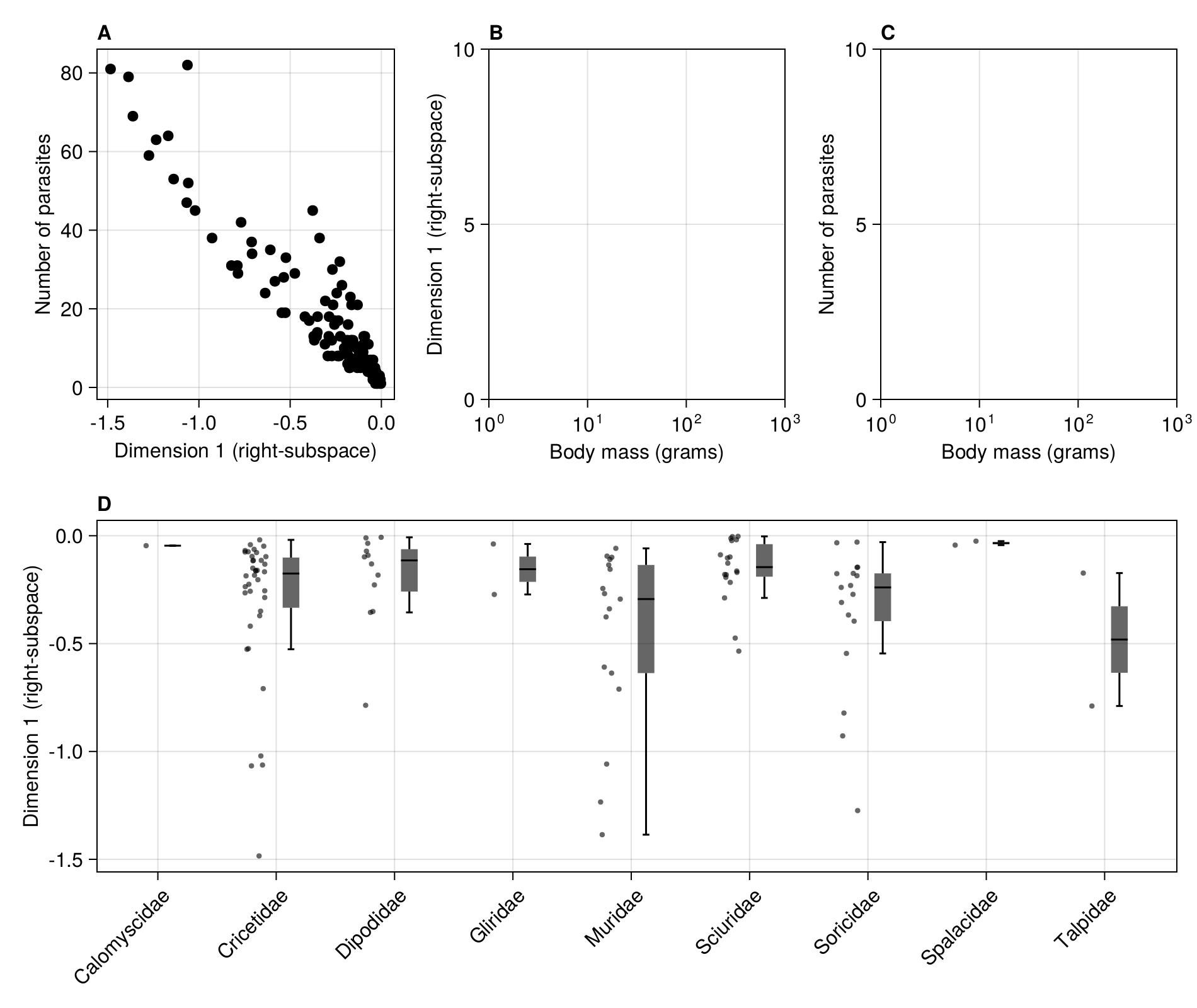

To examine the relationship with functional traits, we remove the species with no known bodymass:

In [143]:
@subset!(rodents, :bodymass .>= 0.0)
67×5 DataFrame
42 rows omitted
Row species family dimension parasites bodymass
String String31 Float64 Int64 Float64
1 Microtus arvalis Cricetidae -1.4844 81 26.9
2 Prometheomys schaposchnikowi Cricetidae -0.0686128 4 75.0
3 Cricetulus migratorius Cricetidae -1.0629 82 30.59
4 Chionomys nivalis Cricetidae -0.0958455 7 42.01
5 Lagurus lagurus Cricetidae -0.2039 10 20.6
6 Cricetus cricetus Cricetidae -0.526361 19 428.95
7 Microtus oeconomus Cricetidae -1.02079 45 33.1
8 Ellobius talpinus Cricetidae -0.113965 9 40.0
9 Microtus agrestis Cricetidae -1.06681 47 35.87
10 Myopus schisticolor Cricetidae -0.370914 13 29.99
11 Mesocricetus brandti Cricetidae -0.224993 13 198.0
12 Microtus socialis Cricetidae -0.264866 21 48.0
13 Alticola argentatus Cricetidae -0.523342 33 37.69
⋮ ⋮ ⋮ ⋮ ⋮ ⋮
56 Sorex isodon Soricidae -0.271786 8 12.23
57 Sorex minutissimus Soricidae -0.367461 12 2.46
58 Crocidura suaveolens Soricidae -0.395894 17 7.35
59 Sorex tundrensis Soricidae -0.17576 5 7.65
60 Diplomesodon pulchellum Soricidae -0.0295968 4 11.0
61 Sorex cinereus Soricidae -0.0326016 1 4.2
62 Sorex roboratus Soricidae -0.239524 8 12.99
63 Sorex alpinus Soricidae -0.230646 8 8.04
64 Neomys anomalus Soricidae -0.185322 6 13.19
65 Crocidura leucodon Soricidae -0.145881 7 10.88
66 Myospalax myospalax Spalacidae -0.0434989 4 225.0
67 Talpa europaea Talpidae -0.789351 31 87.53

And we can finally plot this as the last panel of the figure:

In [144]:
scatter!(
    figure2b,
    rodents.bodymass,
    rodents.dimension;
    color = :black,
)
current_figure()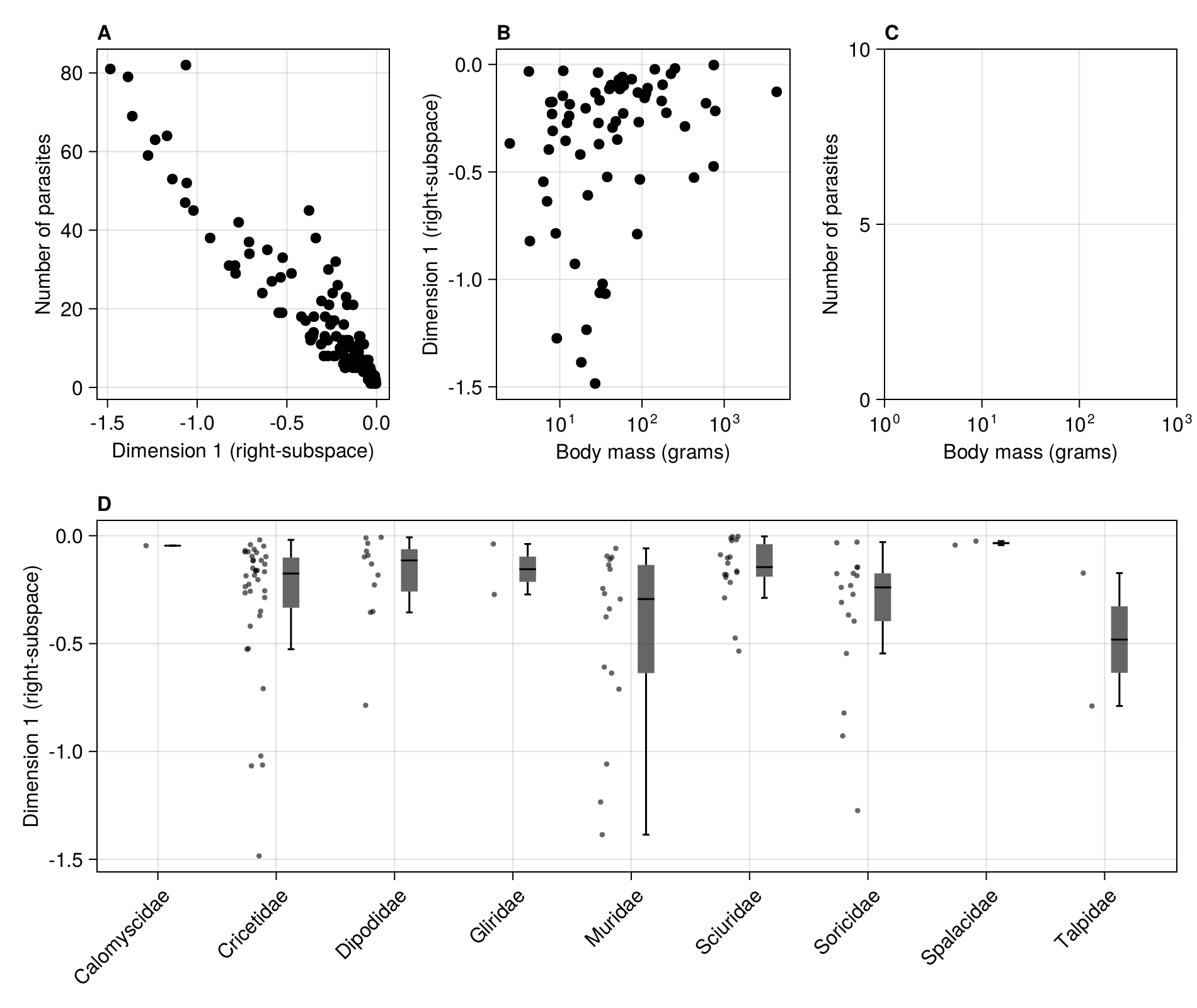

In [145]:
scatter!(
    figure2c,
    rodents.bodymass,
    rodents.parasites;
    color = :black,
)
current_figure()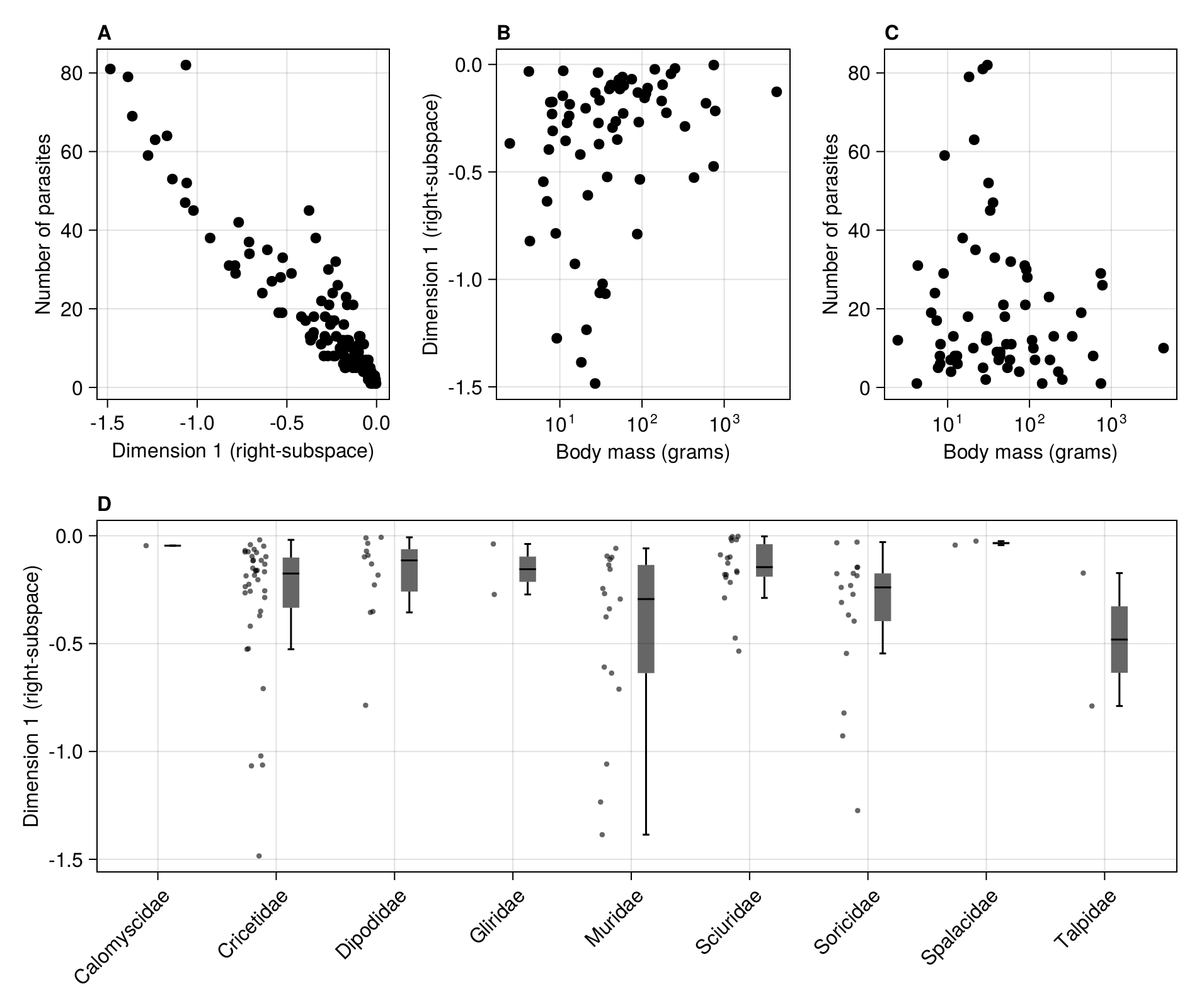

We save the figure to disk in the same way as before:

In [146]:
current_figure()

Figure 2: Ecological analysis of an embedding for a host-parasite metaweb, using Random Dot Product Graphs. A, relationship between the number of parasites and position along the first axis of the right-subspace for all hosts, showing that the embedding captures elements of network structure at the species scale. B, weak relationship between the body mass of hosts (in grams) and the position alongside the same dimension. C, weak relationship between body mass of hosts and parasite richness. D, distribution of positions alongside the same axis for hosts grouped by taxonomic family.